1.はじめに~データ掲載の背景
「esdatapro」は、管理人Kが運営する個人のウェブサイトです。このサイト名は「es」を冠しており、「eSports」に関する多岐にわたる情報を扱うことを目的としています。最近ではCyber Live Arenaのバスケットボールに関する情報も提供していましたが、ブックメーカーでの扱いが終了したため、当サイトでの情報提供も終了しました。
eスポーツに限らず、スポーツ全般において、競技性は大前提です。競技性とは、目的と必要性、そしてそれを支えるインセンティブが重要です。
そんな原則に基づき、この度「E Basketball Battle」(EBB)についても扱うことにしました。EBBは既にβローンチされており、そのデータとはどう考えるべきかを考察し、検証しました。納得のいく結果が得られたため、公式ローンチ前にここでその内容を公開します。
なお、ここでの内容は私個人の考えに基づいており、特定の組織には従属していません。これに共感を持たれた方のみ、本サイトのデータをご活用いただければ幸いです。
2.BasketBallとは
バスケットボールに関するデータを扱う上で、スポーツとしてのその特性を深く理解することが必要です。バスケットボールは、基本的に手を使用するスポーツであり、プレーの精度が高いことが特徴です。これにより、得点の偏差が少なく、試合の結果が予測しやすくなっています。
試合は制限時間内で行われ、シュートクロックも考慮する必要があります。この中で、対戦相手の強みをどう抑制し、弱点をどう突くかが鍵となります。プレーヤーの数が比較的少ないことも、試合の行方を読みやすくする一因となっています。
では、バスケットボールは面白くないスポーツではないかと疑問に思うかもしれませんが、NBAを例にとれば、その答えは「いいえ」です。NBAでは、戦略を超えたプレー、いわゆる「ゾーン状態」におけるスーパープレーが、このスポーツの最大の魅力となっています。
現実のバスケットボールでは、チームの結果や得点に関する予測は比較的容易で、ブックメーカーにとって有利な状況が生まれやすいです。これに対して、ベッターとしての優位性を見出すためには、選手の個人成績(プレイヤープロップ)に焦点を当て、ゲームの背景、コンディション、戦略などを統計データと照らし合わせて判断する方法が主流となっています。
3.E Basketball Battleのデータについて
ここからが重要な部分になります。リアルスポーツにおけるプレイヤープロップが存在しないeバスケットボールでは、ベッティングの項目は、マネーライン(勝敗)、スプレッド(得点ハンデ)、トータル(合計得点)の3つに限られます。
これら3つのベッティング項目に対して適切なデータアプローチを考える際、最初に行うべきは得点分布の把握です。どんな分析手法を試みるにしても、得点がどのように分布しているかを理解することが基本となります。この情報は、それぞれのベッティング項目に対する分析や戦略を立てる上で不可欠です。
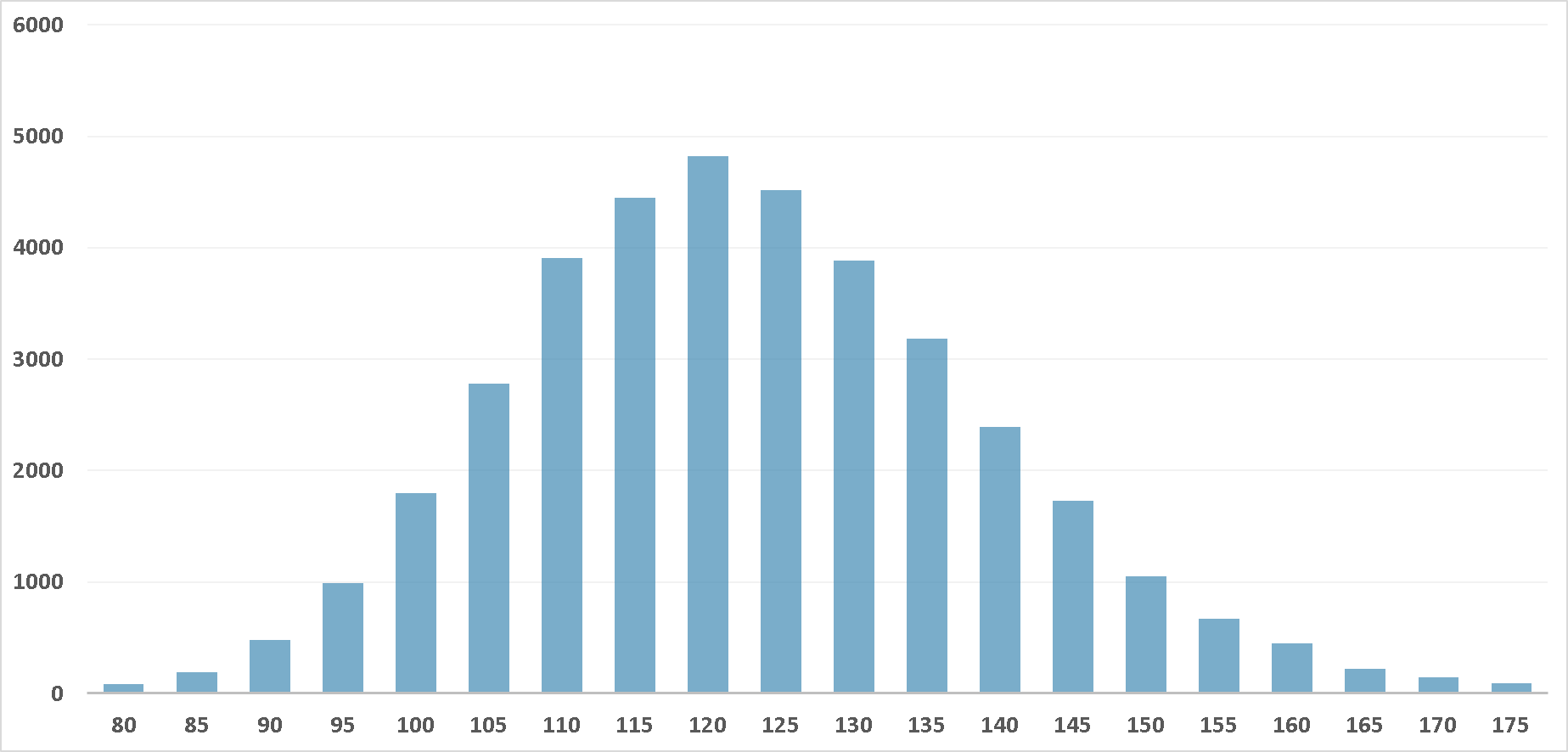
Fig1. EBB合計得点分布図
上記の図は、2022年11月8日から2023年7月15日までに行われた18,596試合のeバスケットボール(EBB)の試合データを基にした合計得点分布図です。この分布図では、合計得点が70点以下および180点以上の試合データは除外しています。除外の理由は、これらの得点範囲のサンプル数が少ないためであり、何ら恣意的な意図はありません。
Fig1を見ると、データは正規分布していると考えられます。多くの統計的検定や推定手法は、データが正規分布していることを前提にして設計されています。データが正規分布に従う場合、これらの手法はより信頼性の高い結果をもたらすことが期待されます。したがって、今後の分析ではこのデータセット(2022年11月8日から2023年7月15日までの18,596試合)を母集団として使用します。
4.分析
前項で触れたように、ベット項目にはマネーライン(ML)、スプレッド(Spred)、トータル(Total)の3つがあります。このうちマネーラインは単純に勝敗を予測するものですが、これには単なる相性だけでなく実力差も含まれます。そのため、データ分析に基づく予想を行う際には、得点と失点の関係性に重点を置くべきです。eサッカーで使用している得失点比率(GF/GA)、勝敗比率(W/L)、得点比率と勝敗比率を合わせたCPを用いて分析を行います。
さらに、今後の分析は7月1日から15日までの試合(合計1,360試合)の結果をもとに行いますが、分析の母集団には当該月の結果も含まれています。このことを考慮に入れながら、データの分析を進めていきます。
Table1. 各比率、CPでの勝敗予想と実績(PTtPT)
| PTtPT※ | True | False |
| GF/GA | 64% | 36% |
| W/L | 65% | 35% |
| CP(GF/GA+W/L) | 66% | 34% |
Table1は、各プレイヤーと使用チームが合致した組み合わせに関して、それぞれの比率およびその合計であるCP(ケミストリーポイント)の優劣を勝敗の実績と照らし合わせた結果を示しています。
この結果から、CPの優劣が勝敗の結果に影響していることが明らかになりました。このため、今後はCPの差異をΔCP(CP差)として分析することになります。このアプローチにより、CPの具体的な影響度と勝敗におけるその重要性をより詳細に把握することが可能になります。
Table2. ΔCPによる勝敗予想と実績(PTtPT)
| ΔCP | Match% | True | False |
| 0.0以上 | – | 66% | 34% |
| 0.5以上 | 62% | 71% | 29% |
| 1.0以上 | 38% | 75% | 25% |
| 1.5以上 | 18% | 78% | 22% |
| 2.0以上 | 13% | 79% | 21% |
| 2.5以上 | 7% | 83% | 17% |
| 3.0以上 | 7% | 83% | 17% |
| 3.5以上 | 5% | 85% | 15% |
| 4.0以上 | 2% | 87% | 13% |
| 4.5以上 | 1% | 94% | 6% |
| 5.0以上 | 1% | 89% | 11% |
Table 2のデータを分析すると、ΔCPが大きくなるほど勝率が上昇し、その間に比例関係が存在することが明らかになります。さらに、ΔCPの分布を試合数割合で見ると、ΔCPが0.5以上の試合が全体の約62%を占めており、これらの試合の勝率が71%であることが分かります。これを踏まえると、期待値はおおよそ2.13程度(1/(66%×71%))が必要となると考えられます。この分析は、ベッティング戦略を練る際に非常に重要な指標となります。
ここまではPTtPTの結果を見てきましたが、ここでPTtPTとPtPの結果を比較してみます。
Table3. PTtPTとPtPのCP勝率比較
| Case | True | False |
| PTtPT | 66% | 34% |
| PtP※ | 59% | 41% |
チーム差を排除したプレイヤー間の直接対決とCP勝率を比較すると、PTtPTの優位性が確認できます。これは、プレイヤー間の相性だけを理解しても勝率を高めることはできず、チームの理解が勝率向上に重要な役割を果たすことを意味します。
一方で、チーム理解に関しては、深い理解を追求するのが理想ではありますが、最低限、ゲーム上でどちらのチームが強いかを知るだけでも十分であると考えられます。
ここまでの分析は勝敗に焦点を当ててきましたが、次は得点に関する分析に移ります。読者の中には「もう十分だ」と感じる方もいらっしゃるかもしれませんが、もう少し詳しく見ていきましょう。
得点関連では、主流はトータルオーバー/アンダーです。前述したように、合計得点数の分布が正規分布に基づいていると仮定して、95%信頼区間について分析と検証を行います。
Table4. 95%信頼区間の比較(PtP,PTtPT)
| LL95% | UL95% | |||
| Case | TRUE | FALSE | TRUE | FALSE |
| PtP | 59% | 41% | 60% | 40% |
| PTtPT | 73% | 27% | 72% | 28% |
Table4は、サンプルの標準偏差を既知として95%信頼区間を算出し、実績と比較した結果を示しています。この結果から、PtPよりもPTtPTの方が優れていることが分かりますが、なぜサンプルサイズ(サンプル数)がPtP > PTtPTであるにも関わらず、PtPの精度が劣るのでしょうか。
この疑問に対して行った調査によると、母集団数とサンプルサイズの間には以下のような関係が存在します。
Table5. 母集団数とサンプルサイズ
| 母集団数 | サンプルサイズ |
| 100 | 80 |
| 1,000 | 278 |
| 10,000 | 370 |
| 100,000 | 383 |
| 1,000,000 | 384 |
Table 5は、誤差率5%、信頼率95%を実現するために必要な母集団とサンプルサイズの関係を示しています。サンプルサイズの算出には特定の計算式が用いられ、母集団の数と各要求パラメータによって決定されます。
Table 5によると、母集団の規模が大きくなるにつれて必要なサンプル数が増加することが分かります。母集団が10,000を超えるとサンプルサイズの増加は著しく鈍化し、母集団に対するサンプルサイズの割合が小さくなる傾向が見られます。
この理論を適用すると、誤差率5%、信頼率99%(既に5%の誤差を許容しているため)の場合、18,596試合の母集団に対して必要なサンプル数は641試合となります。
PtPでは、United Centerでの試合をサンプルとすると、2022年11月以降のデータでは約400試合となり、必要なサンプル数には達していません。PTtPTでは、PtP以上にサンプル数が不足していますが、PTtPTの方が精度が高い理由は、サンプルの質にあると考えられます。
合計得点数の標準偏差を比較すると、PtPよりもPTtPTの方が約30%低いことが分かり、使用チームの影響が無視できないことが明らかになります。
これらの結果から、95%信頼区間の適用はサンプルサイズが不足しており適切ではないことが判明しました。そのため、次にはよりシンプルな分析方法を採用します。
Table6. 最大(最小)値による区間算出実績比較
| min95% | min90% | max90% | max95% | |||||
| TRUE | FALSE | TRUE | FALSE | TRUE | FALSE | TRUE | FALSE | |
| PtP | 95% | 5% | 91% | 9% | 90% | 10% | 95% | 5% |
| PTtPT | 82% | 18% | 71% | 29% | 68% | 32% | 82% | 18% |
表6は、簡単に述べると、最大値(最小値)の95%を計算し、その結果をトータルのオーバー/アンダーの実績と比較したものです。 PtPの場合、的中率が高くなる傾向が見られます。これは非常に当然の結果で、サンプルサイズが大きいために最大値(最小値)も増大し、その結果95%分布の範囲が広がるためです。この広がった範囲に結果が収まりやすくなりますが、その反面、オッズの発生頻度は低下します。
また、これまでの分析でPTtPTの有利性が証明されているため、トータルにおいてもPTtPTを用いて勝ち筋を見極めることが重要になります。このため、勝率の高いPTtPT/min95%について、試合数別にさらなる分析を行います。
Table7. match数と勝率の関係(PTtPT/min95%)
| PTtPT | Match% | TRUE | FALSE |
| 0以上 | – | 82% | 18% |
| 10以上 | 71% | 87% | 13% |
| 20以上 | 32% | 88% | 12% |
| 30以上 | 11% | 93% | 7% |
| 50以上 | 5% | 97% | 3% |
Table7は、PTtPTのマッチ数とmin95%勝率の関係性を分析したものです。この分析から、PTtPTのマッチ数が多いほど勝率が高くなる傾向が明らかになりました。TotalのOver/Underにおいては、最大値(または最小値)の更新をどう避けるかが重要です。この点に関して、母集団内での最大値更新頻度を調べた結果、全18,596試合のTotalを順番に並べた時、最大値が更新されたのは合計14試合だけでした。
特に、最初の10試合で2回、20試合までに1回更新された後、100試合までの間は約10試合に1回の頻度で最大値の更新が見られましたが、その後は更新頻度が収束していきました。これにより、10試合以上のマッチを選ぶことが妥当だと考えられます。
以上の分析結果から、PTtPTが10試合以上の組み合わせの場合、最小95%の期待値が約1.4(1/(82%×87%))程度になると予測できます。これは、ベッティングにおいて充分なエッジを得られる可能性があると考えられます。
おわりに
ここまでの分析と検証をまとめると以下のとおりです。
- 使用チーム影響は大きい
- MLはΔCP0.5以上の試合で期待値2.13以上が合理的な結果を示している
- 得点データは正規分布しているものの、統計検定手法や推定手法を適用するにはサンプルサイズが不十分
- Total Over/Underは、最大値更新頻度を避けるため、PTtPT10試合以上を選定
これらの分析と検証を踏まえ、EBBにおける理論的な勝利の道筋(長期的な利益)を確立できたため、本日(7/22)より、当サイトでのEBBデータの公開を正式に開始します。
理論値はあくまで理論上のものであり、背景の確認や映像の精査が重要であることに変わりはありません。やる気のなさは統計的に見て過誤、いわゆるエラーにあたります。これを避けるためにも、これらの要素は重要です。
また、統計検定や推定手法が適用できないサンプルサイズであることの理解が深まりましたが、それと同時に大規模な母集団データの重要性も明らかになりました。要するに、恣意的な期間でデータを抽出することは避けるべきだということです。
そして、最も重要なのはチーム理解であり、これが結果と理論値において証明されました。これは今後の分析においても変わらない価値観となるでしょう。
私自身はEBBのベットにはあまり参加していないため、実感が伴っていませんが、今後はこれを機にEBBをより注目していこうと思います。本サイトを利用してEBBに取り組む方々の体験談を伺えれば幸いです。ただし、実感を得るまでは少額の投資を推奨します。
K